힙&이진탐색트리

트리(Tree)

• 루프를 갖지 않고 연결된 무방향 그래프 구조 
• 트리내에 또 다른 트리가 있는 재귀적 자료구조
• 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖는다.
• 사용 예: 디렉터리 구조, 조직도

  

  이진 트리

  
  

힙(Heap)

개념 및 특징

• 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리
• **완전 이진트리란? 단 두개의 자식 노드만 갖는 이진 트리 중 노드가 왼쪽부터 차례로 채워져 있는 트리 
• A가 B의 부모노드이면, A의 키 값과 B의 키 값 사이에는 대소관계가 성립한다. => 형제 사이에는 대소관계x
• 부모노드의 키 값이 자식노드의 키 값보다 크거나 같은 완전 이진 트리를 '최대 힙(max heap)', 작거나 같은 완전 이진 트리를 '최소 힙(min heap)'이라고 한다. 
• 우선순위 큐를 구현하는 데 사용된다. 
• 중복된 값을 허용한다.

  

  이미지 출처 https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

구현

• 일반적으로 배열로 간단하게 구현
• 왼쪽 자식 노드 index = 부모 노드 index * 2
• 오른쪽 자식 노드 index = (부모 노드 index * 2) + 1
• 부모 노드의 index =  자식 노드 index / 2

동작 과정

• 데이터의 삽입
  1. 인덱스 순으로 가장 마지막 위치에 이어서 새로운 요소를 삽입한다.
  2. 부모 노드와 값의 크기를 비교해서 서로 교환한다.
  3. 자신의 위치를 찾을 때까지 2번 단계를 반복한다. 
• 데이터의 삭제 
  1. 루트 노드를 삭제한다. (최대 힙에서의 삭제 연산은 최댓값을 가진 요소를 삭제하는 것)
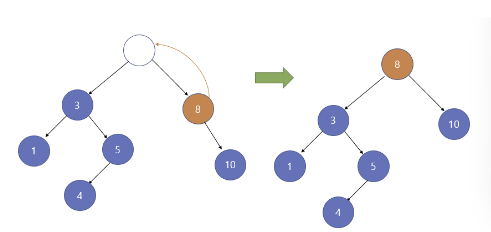
  2. 힙의 마지막 노드를 루트 노드로 가져온다. 
  3. 자식 노드와 값의 크기를 비교해서 서로 교환한다. (힙을 재구성)

시간 복잡도 

• 삽입: O(logN) 
• 삭제: O(logN)

 

이진 탐색 트리

개념 및 특징

• 모든 원소의 키는 유일한 키를 가진다. (힙과의 차이)
• 왼쪽 서브트리에 있는 키들은 그 루트의 키보다 작다.
• 오른쪽 서브트리에 있는 키들은 그 루트의 키보다 크다. 
• 왼쪽, 오른쪽 서브트리도 모두 이진 탐색 트리이다. 
• 중위 순회(inorder)로 정렬된 순서를 읽을 수 있다.

이미지 출처 https://dream-and-develop.tistory.com/146

동작 과정

• 데이터의 삽입
  1. 삽입할 값을 루트 노드와 비교해 같으면 오류 발생
  2. 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있으면 추가, 그렇지 않으면 다시 비교
  3. 루트 노드의 키보다 크다면 오른쪽 서브트리를 탐색해서 비어있으면 추가, 그렇지 않으면 다시 비교
• 데이터의 삭제
  • 삭제하려는 노드가 단말 노드인 경우
    • 삭제할 노드의 부모 노드가 있다면 부모 노드의 자식 노드를 NULL로 만들고, 삭제할 노드를 삭제
  • 삭제하려는 노드의 서브 트리가 하나인 경우(왼쪽 or 오른쪽 서브 트리)
    • 삭제할 노드의 자식 노드를 삭제할 노드의 부모 노드가 가리키게 하고 해당 노드를 삭제 
  • 삭제하려는 노드의 서브 트리가 두 개인 경우
    1. 삭제할 노드의 왼쪽 서브 트리의 가장 큰 자손을 해당 노드의 자리에 올린다. 
    2. 삭제할 노드의 오른쪽 서브 트리의 가장 작은 자손을 해당 노드의 자리에 올린다. 

1번 방법

 

2번 방법

시간 복잡도 

• 균등 트리: O(logN)
• 편향 트리: O(N)

 

참고

https://code-lab1.tistory.com/10

[자료구조] 이진탐색트리(Binary Search Tree)의 개념, 이해 | C언어 이진탐색트리 구현